Introduction

One of the main goals of separation sciences today is reconstructing natural carriers or ducts through artificial design. An essential step in achieving this goal is to replace natural carriers with simpler analogs. In fact, biomimetic approaches to generate artificial analogs allow us to create artificial supramolecular structures that can mimic biological functions. There are several advantages to using artificial channels, which among the most important ones are simple structures, adjustability, durability, stability, and compatibility with membrane host matrices. Artificial water channels (AWCs) have been developed1,2 in the hope of making synthetic analogs of natural aquaporins (AQPs) proteins that can act in terms of water permeability or even selectivity better than natural aquaporins. Since the transfer of water through artificial channels is vital for a cell’s function, in 19923, Peter Agre explored a protein heterodimer that carries water molecules across cell membranes through water channels called aquaporins. One obvious advantage of AWCs over natural aquaporins is that they are easily moldable and rigidly fixed in the membrane structures, so it can be expected that the utilization of AWCs will lead to the formation of high permeability layers with excellent salt excretion. In AWC systems, water molecules are transported into the inside or outside of the cavities’ channels in the form of water wire structures. In other words, the transfer of water clusters depends on the internal diameter of the channel’s pore, which can increase or decrease water permeability. In addition, the weak interactions between hydrophobic walls of the channels and water molecules help the water molecules to move without friction, while the selectivity is controlled by the steric effects4,5. Increasing water infiltration into the canal or improving salt excretion is a real challenge to increase the efficiency of AWCs6. Obtaining absolute water selectivity in designing a channel, depending the ability of H-bonding between the water molecules and the pores of channels, which mainly causes water to penetrate within the channel. Therefore, water is transported via H-bonds as a donor and acceptor and forms water wire, where the inner pores of the AWC channels contact a water molecule. Recently, more computationally efficient strategies have been developed to model the structural and dynamic properties of water molecules in protein channels such as aquaporin. For example, Song et al. examined cluster-forming organic nanoarchitecture, peptide-appended hybrid arene (PAH)7, as a modern class of artificial channels for the transfer of water molecules. The results of fluorescence experiments and simulations revealed that PAHs form clusters that can penetrate the lipid membranes and prepare synergistic membrane-spanning paths for selective and rapid water permeation via water-wire networks. Besides, Maurin et al.8 discussed the biomimetic imidazole (I)-quartz quartets obtained from self-assembly of alkyl-ureido-ethyl-imidazoles HC4−HC18 in bilayer or polyamide (PA) membranes. They found that the various I-quartets with different hydrophobic tails could significantly increase single-channel water permeability through enhancing the size of the alkyl tail. Therefore, by evaluation of AWC−PA nanochannel, they reveal that the generation of nanoscale sponge-like water channels could be obtained with low dispersed, low soluble, and insoluble artificial water channels. Barboiu et al.9 reported that the artificial I-quartz channels, similar to AQP channels, can be encapsulated dipolar water wires inside the I-quartz conduit. In this regard, they performed X-ray structural analyses, bilayer transport experiments, and also classical molecular dynamic (MD) simulations to gain key insights into biological systems and quantify transport. They found that these channels are able to selectively transport the water molecules every second while rejecting all ions. Their results confirmed that the behavior of ions in these channels plays important role in the systematic detection of artificial water channels for desalination.

Barboiu et al.4 have reported AWCs based on octyl-ureido-polyol that can be formed through the self-assembly of hydrophilic hydroxyl channels, to regulate the water transport permeability, with the rejection of ions. They indicate that similar structural features as found in the natural aquaporins pores, with a central pore size of ~3.5 Å, which AWCs is mimic the aquaporin’s channel. The results of their work confirmed that the advantages of hydrophilic channels are related to the interactional nature of the channel cavity via interaction with the transport of water.

The water hardness is mainly measured based on the two metal ions, magnesium, and calcium. Although other ions such as aluminum, sodium, chlorine, manganese, and zinc exist in hard water, is known that the values of calcium and magnesium ions are the highest. In addition, what is certain is that the calcium and magnesium ions in hard water have the most destructive effects on the environment. Moreover, the high concentration of nitrate ions has potential risks and creates high toxicity in drinking water, groundwater, aquaculture wastewater, secondary effluent, and wastewater. Based on our knowledge, the removal of calcium, magnesium, and nitrate ions is preferred from hard water.

In this study, a series of MD simulations and well-tempered metadynamics (Wt-metaD) simulations are performed in a membrane environment that allowed us to investigate a range of permeation scenarios with the transport of various compounds at the lipid boundaries. These simulations help to filter out ions and also pass water molecules through the artificial channel cavity and provide an accurate view of putative permeant channels to water-filled channel transport. Inspired by these biological channels, they can also be used in large-scale industrial applications with entirely different physical and chemical environments.

This insight opens up new avenues in AWC research toward the selection of biochemically inspired membranes for desalination. These biological channels also create new possibilities for further research to better understanding the selection details of these aquaporin channels. Inspired by these biological channels, we decided to investigate an artificial channel for water treatment by rejecting ions such as calcium ions, nitrates, and so on.

Overall, a full dynamical description of the biomolecular events can be obtained via the run of the MD simulations with various degrees of accuracy10,11,12,13. In fact, in this study, we intend to answer the question: Is it possible to observe the spontaneous formation of water wires via MD simulations?

Result and discussion

MD simulation

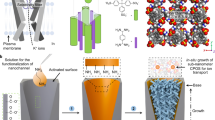
We carried out MD simulations to understand the ability of the OH artificial channel toward permeability and transfer of water molecules. We herein report a new class of AWCs based on octyl-ureido-polyols (H4) for the removal of ions, which have hydrophilic hydroxyl groups, and also can self-assemble to form hydroxy OH Channel, as shown in Fig. 1. The distance between the same monomers of the water channel is ~3.5 Å, which makes up the water passage. Our simulations can be divided into three parts to determine the transport of water along with the removal of the ions through the OH channel for water treatment: (a) OH channel/magnesium ions in solution, (b) OH channel/calcium ions in solution, and (c) OH-channel/nitrate ions in solution. The initial and final snapshots of the 60 ns MD simulations are presented in Figs. 2, 3, also final snapshots of AWC/Na+ and AWC/Cl− systems are depicted in Supplementary Fig. 1. As shown in Fig. 2, this simulation box consists of three parts: from left to right in the Figure, pure water, the OH channel, and the impure water, respectively. From the final snapshots (Fig. 3), it is found that after 60 ns, water molecules transfer from the concentrated solution to the dilute solution, and during the simulation period, interestingly no ions penetrated the channel. In addition, in system C, the OH channel has a high selectivity for translating water molecules than the other systems, and the water molecules form stronger interactions within the pores of the OH channel. This behavior can be attributed to the smaller size of Ca2+ ions, leading to greater mobility of these ions and causing the water molecules around them to become less hydrated. Therefore, the water molecules have more freedom to move and penetrate the pores of the OH channel.

Fig. 1: The structure of OH channel.
figure 1

(a) The self-assembled OH channel, (B) the monomer of OH channel, color codes: O: red, N: blue, C: cyan, H: white.

Full size image
Fig. 2
figure 2

A sample of the initial simulation box before each simulation run.

Full size image
Fig. 3: The final snapshots of the studied systems after 60 ns MD simulation.
figure 3

A) system C, B) system B and C) system A.

Full size image

In addition, about AWC/Na+ and AWC/Cl− systems, as seen from the final snapshots in Supplementary Fig. 1, the Na+ and especially Cl− ions passed through the channel along with water molecules during the simulation time. In fact, this behavior can be attributed to the small size of the sodium and chlorine ions, which leads to a higher movement speed of these monovalent ions so that they can move more freely. Therefore, it causes these ions to be less hydrated via the water molecules and makes powerful penetration into the AWC pores.

It should be noted that the existence of C=O, O-H, and NH groups on the monomers of the channel makes it hydrophilic and thus has a tendency to swell and adsorb water. In addition, monomers of the membrane form HB together and also cause the structure of the channel slightly swelled. This finding is also evident in Figs. 1, and 2.

To further investigate the OH channel’s ability to transfer the water molecules and remove the ions, different types of analysis are carried out as follows.

The non-bonded interactions, such as van der Waals and Coulombic interactions are calculated, and the values of non-bonded interaction energies for the three different systems over the simulation time are given in Table 1; and also, the interaction energies for both AWC/Na+ and AWC/Cl− systems are given in Supplementary Table 2. Also, the averaged interaction energies for the water molecules and the AWC presented in Fig. 4; as well, the total interaction energies between water molecules and ions (Na+/Cl−) with AWC are depicted in Supplementary Fig. 2. As shown in Table 1, the values of electrostatic energies are more than van der Waals (vdW) energies, as well as, the electrostatic interactions play a much more prominent role in all studied systems. The electrostatic interactions of ACW/water molecules shows different negative values in the following order: system-C > system-A > system-B (B: −1669.8 < A: −3114.94 < C: −5084.74 kJ mol−1), also, for AWC/Na+ and AWC/Cl− systems, the electrostatic interactions are about −2841.73 and −820.101 kJ mol-1, respectively. A careful examination of Table 1 shows that the water molecules have good stability when passing through the narrow regions of the channel pores, leading to regions of a high density of water. This phenomenon can be related to the strong hydrogen bond interaction between the hydroxyl-rich pores of the OH channels and the water molecules. On the other hand, the water molecules can act as acceptor and donor H-bonds and form a considerable of hydrogen bonds within the active site of OH channels. In system A, which contains nitrate ions, the value of electrostatic energy is about −466.473, while in both other systems intended to zero. The increase in electrostatic energy is most probably because the nitrate ions can form the H-bond with both entities (water and AWC).

Table 1 The L-j, electrostatic and total energies (all in (kJ mol−1)) of the three studied systems.
Full size table
Fig. 4: The interaction energy between water molecules and AWC.
figure 4

The error bars represent the standard deviations of the data.

Full size image

As seen from Supplementary Table 2, the values of negative electrostatic energy (elec) for the interaction of ions with AWC confirm that the monovalent ions can pass through the channel pores along with the water molecules. However, the values of interaction energies for the Cl− ions in the AWC/Cl− system are more negative in comparison to the Na+ ions in AWC/Na+. Therefore, the results showed that the hydroxy filtration channel is not useful for the removal of sodium and chlorine ions because the sodium ions, especially chlorine ions, easily accompany the water transfer process.

By monitoring the time dependence root mean square deviation (RMSD), the stability and conformational changes of the AWC channel can be investigated. The RMSD of the studied systems is evaluated and presented in Supplementary Fig. 3. As it is obvious from this figure, after 10 ns, the RMSD of the investigated systems remained stable until the end of the simulation time. In fact, the monomers of AWC are set into stable sites along each other, where each monomer is in contact with the adjacent monomers. Consequently, their structure remains regular until the end of the simulation time, at 60 ns.

Water translational dynamics

To obtain the relative mobility of water molecules and selected ions in the investigated systems the mean square displacement (MSD) is calculated based on Eq. (1).

$${{{\mathrm{MSD}}}}({{{{t}}}}) = \frac{1}{N}\mathop {\sum}\limits_{i = 1}^N \left\langle { {[ {r_i(t_0 + t)^2}]}\left. - r_i(t_0) \right]^2} \right\rangle$$
(1)

where ri(t) is the molecule position i at time t, hence ri(t0) is the initial position, the angular bracket represents the ensemble average over time, and N denotes the number of atoms.

Figure 5 presents the MSD curves for the water molecules and selected ions along the z-axis of the pores in the simulated systems. The MSD curves of each system indicate that the molecules in the different systems have different diffusion tendencies. As it is obvious from the interaction energy values, the MSD curve for the magnesium ions locates at a much higher position compared to other ions. This behavior results from the stronger repulsive interactions between the divalent cations Mg2+ and the AWC nanochannels. These features can be attributed to the small size of Mg2+ ion, higher charge density, and higher hydration energy. It means that the magnesium ions attract water molecules to form a hydration structure, therefore having less penetration into the pores of the nanochannel. It’s worth mentioning that the different ions in each simulation box cannot penetrate into the pores and are mainly located on the outer surface of the AWC. However, systems A and C have similar curves of water diffusivity and show an abrupt decrease in comparison to the MSD curves of ions/AWC (Fig. 5). It shows an increasing order of self-diffusivity of water in the pores and can be concluded that the AWC nanochannel encapsulated water wires or clusters, offering iterative and continuous H-bonding with the water molecules. Since the MSD curves do not have any fluctuation, it can be assumed the systems reach convergence and steady state during the water diffusion into the channel. This finding confirms that the systems tend to converge and get stable; thus the model that is established can be used for application in the removal of toxic ions from water.

Fig. 5: MSD pattern.
figure 5

Time evolutions of MSD for the different ions and water molecules in the simulated systems.

Full size image

Besides, Water self-diffusion coefficients (Di) for systems A, B, and C have been predicted using the Einstein relation14 Eq. (2):

$${{{{D}}}}_i = \mathop {{\lim }}\limits_{t \to \infty } \frac{1}{{6N_mt}} \left\langle \mathop {\sum}\limits_{i = 1}^N {[r_i(t) - r_i(0)]^2} \right\rangle$$
(2)

where ri(0) and ri(t) are the positions of the center of mass of the molecules at time 0 and t, respectively; N is the total number of molecules, and <> means an ensemble average, Di is the self-diffusion coefficient. The Di of the water molecules for systems A, B, and C are 50.0726, 5.7431, 71.2029 (10−10 (m2 s−1)), respectively, as illustrated in Fig. 6. As expected, the above data demonstrate that the coefficient Di for water molecules in the presence of calcium ions has a significant amount.

Fig. 6: The self-diffusion coefficient.
figure 6

The Di value of water molecules in different systems.

Full size image

In the case of the Cl− and Na+ ions, their quick motion reduces their hydration via the water molecules; and increases the rate of Na+/ Cl− ion’s passage into the hydroxy channel pores. This phenomenon leads to a larger coefficient Di for water molecules in anions system than in cations system, especially for Cl− ions ((Di(Cl−) = 64.5318 10−10 (m2 s−1) and Di(Na+) = 4.9354 10−11 (m2 s−1)), see Supplementary Fig. 4) fig. 7.

Fig. 7: Density profile.
figure 7

The profile density of water molecules toward OH channel.

Full size image

Density profile

The density profile can be defined as measuring the probability of water being present at a specific location. Therefore, the density profile of water molecules for NO3−/water, Ca2+/water, Mg2+/water systems in the z-plane of the substrate is calculated, it is noted that both sides of the channel are inaccessible for the water molecules. In fact, the density profile (ρ) is considered because the water concentration is changing in the various systems (ρ is the density of water molecules). The density distribution of water molecules across the OH-channel is presented in Fig. 7. As seen in this Figure, the five oscillating density peaks are observed for each system, implying five-layer structures of the OH channel that confined water molecules. The distributions of water molecules are highly symmetric near the surface along with multiple peaks, which reflect the effect of the AWC channel on the transferred water flow. Additionally, the five peaks at short range mirror local hydrogen bonding structure, with the first hydrogen bond peak appearing approximately at 1.5 nm for systems A and C, as well as 2.5 nm for system B, as expected. While the general forms of the density profiles are essentially the same but observed that the highest peak belongs to the systems C with a height of about 70 kg m−3.

Fig. 8
figure 8

Pure water flux for the OH channel in the studied systems.

Full size image

Water flux

The pure water flux (PWF) is calculated to examine the water permeability of the OH-channel and is obtained based on Eq. (3):

$${{{{J}}}}_{{{\mathrm{w}}}} = \frac{V}{{A \times t}}$$
(3)

where JW is PWF (L m−2 h−1), V is the volume of solution in permeated water, A are the effective area and t is time (h).

It is worth mentioning that when a net water flow (filtration and/or osmosis) across a membrane and a permeant solute exists, a solute flux in the same direction is present as the water flow. This flux reflects water-solute frictional interaction within the membrane. The solute flux is calculated by using Eq. (4):

$${{{{J}}}}_{{{\mathrm{S}}}} = {{{{J}}}}_{{{\mathrm{v}}}}\,{{{{C}}}}_{{{\mathrm{v}}}}\,(1 - \sigma _{{{\mathrm{s}}}})$$
(4)

Pure water flux results for OH-channel membranes are presented in Fig. 8. The obtained results showed that the Jw for the most stable structure, i.e. system C, is about 20.2 (L m−2 h−1) and for A and C systems are 19.08, 17.96 (L m−2 h−1), respectively. As can be seen from Fig. 8, adding Ca2+ increases the water flux compared to the other ions. It is worth mentioning that the increase in the water flux was due to the greater mobility of Ca2+ ions, which leads to these ions becoming less hydrated, so more water molecules penetrate the pores of the OH channel. It is worth noting that in simulated systems, all the ions accumulate at the top of the channel cavity, and they are not transferred into the OH-channel membrane. Therefore, for all studied systems, the solute flux is close to zero.

Rejection of Ca2+, NO3−, and Mg2+ ions from the OH-channel membrane can be calculated using the following Eq. (5):

$${{{\mathrm{Rejection}}}}\,\left( {{{\mathrm{\% }}}} \right) = \left( {1 - \frac{{C_{\rm{p}}}}{{C_{\rm{f}}}}} \right) \times 100({{{\mathrm{\% }}}})$$
(5)

where Cp and Cf are the concentrations of ions (Ca2+, NO3−, and Mg2+) in the permeate side and initial feed side, respectively.

According to this Equation, the rejection rate of these ions from the hydroxy channel is about 100% for Ca2+ and Mg2+, and 67% for NO3−, respectively.

Numerous studies have reported the values of pure water flux as a function of permeability and selectivity of water molecules. To verify our simulated systems are in line with other lectures, the obtained pure water flux of our work is compared with prior studies. Zhang et al.15 designed the reverse osmosis membranes, thin film nanocomposite reverse osmosis membranes coated by functionalized multi-walled carbon nanotubes (MWNTs), to enhance the water flux of osmosis membranes. Their results show that modified MWNTs might play the role of water channel, and also, the water permeability increases from 26 L m−2 h−1 to 71 L m−2 h−1. Moreover, the NaCl rejection of MWNT-polyamide membranes decreases in compression to the bare polyamide membrane. Bandehali et al.16 used zinc oxide (ZnO) nanoparticles and functionalized them via glycidyl POSS to prepare polyether-imide based-nanofiltration membranes (POSS-ZnO (PZ)). The effect of different concentrations of POSS-ZnO (PZ) membranes is evaluated to investigate their capacity for separation performance and antifouling properties. The highest pure water flux (42.4 L m−2 h−1) is observed for M1-PZ in 0.001 wt% of PZ nanoparticles, while this value reaches 17 (L m−2 h−1) for neat membrane and 12–18 (L m−2 h−1) for PEI/ZnO, respectively. Liang et al.17 employed graphene oxide (GO) as a high-performance separation membrane by forming tunable and ordered nanochannels. They found that the proposed channel structure facilitates water-selective sorption and achieved the superior performance GO membrane with a flux of 5.94 L m−2 h−1 and a water/butanol separation factor of 3965. Also, Sapkota et al.18 used Molybdenum disulfide (MoS2) laminar membranes with porous nanosheets (NSs) graphene-based membranes for water desalination in commercial water purification applications. Their results in forwarding osmosis showed that membranes reject more than 99% of salts at high salinities. Furthermore, water flux in a porous MoS2 membrane is about 70% higher than in a porous graphene membrane. In another study, Mohamed E.A. Ali et al.19 investigated the effect of certain organic acids, acetic acid, methacrylic acid, and tartaric acid, doped in polysulfone (PSF) solution on the efficiency of the nanofiltration (NF) membranes. They found that the water flux and salt rejection in a polysulfone/methacrylic acid (PSF/MAAc), polysulfone/tartaric acid (PSF/TAc), and polysulfone/lactic acid (PSF/LAc) membranes are about 16.8, 18.5, and 20.2 L m−2 h−1 and 8, 88.2 and 94.1%, respectively. They also investigated a new chemical and surface modification for thin-film composite (TFC) membranes through redox, and interactions with Cu2+ ions in CuCl2 solution to improve the water flux, salt rejection, and chlorine resistance of TFC membranes20. Their results confirmed that the mineralized membrane with optimum concentrations of copper chloride and ammonium hydroxide had a higher pure water permeability and solute water flux (44.25, 33.77 L m−2 h−1) compared to the pristine TFC membrane (21.36, 20.2 L m−2 h−1) with an excellent salt rejection (≥98.5 %).

Close inspection of the obtained results shows that the water flux in the most stable structure (System-C) in this study is in good agreement with the recent experimental work reported by Mohamed E.A. Ali et al.19,20 Bandehali et al.16.

Computation of pair distribution functions

Radial distribution function (RDF) is a suitable tool for describing the distribution of a guest molecule around a host surface; in essence, this work of describing the transport of water molecules in the OH nanochannel. In this regard, the RDF pattern can provide us an important insight towards the understanding of the accumulation as well as the transfer of water molecules concerning the AWC. Results of RDF analysis in the investigated systems are given in Fig. 9. As seen in Fig. 9 and Supplementary Fig. 5, in the short distance, the RDF is zero, and the sharp peak is not observed in this region, which is due to the strong repulsive forces between the water molecules and AWC pores in the short range (>0.2 nm). The RDFs between the water molecules and the skeleton of AWC show distinct peaks, the height of their peak is ordered as system C > system A > system B, illustrating that system B has the weakest water transport into OH-channels; as well AWC/Cl− > AWC/Na+ systems (see Supplementary Fig. 5).On the other hand, in system B, some of the water molecules are attracted by the Mg2+ ions, that is, the number of water molecules available in pores of the channel decreases. However, the highest peaks belong to system C and AWC/Cl− system, which appeared at around 0.4–0.6 and 0.5 nm, respectively. That is related to the hydration of existing ions in the system, where the coulombic interaction among water molecules is much higher than that of ions. (ref. Table 1 and Supplementary Table. 2). A close inspection of Fig. 9 indicates that the peak intensity in system A is similar to system C. These observations are in agreement with the results of the energy obtained, indicating the important role of the electrostatic term in the transport of water molecules.

Fig. 9: RDF pattern.
figure 9

The RDF of the water molecules around the OH channel.

Full size image

Hydrogen bond network

Hydrogen bonds formed between the interface and adjacent water molecules are among the main factors contributing to the clean water flux in the process of ion excretion. Based on a donor-acceptor cutoff distance of 3.5 Å, the hydrogen bonds analysis is assessed, and their role in the distribution of water molecules is evaluated. Supplementary Fig. 6 provides the number of hydrogen bonds (HB) presumably formed between the water molecules and AWC in the studied systems. It can be seen from Supplementary Fig. 6 the average number of hydrogen bonds progressively increases from 0 to 400 as water molecules are transferred from impure water above the substrate to the pores of the channel and pure water. In fact, the water molecules enter the AWC channel by the adsorption force induced by hydrogen bonding, subsequently starting the wetting, and transport process. In other words, the enhancement in the bulk density of water molecules around and inside the OH channel is influenced by the Coulombic force from the hydrogen bonding network effect of the hydroxyl groups of the channel. As seen, in system C, owing to the weakening attraction effect of calcium ions away from the OH-channel substrate, water molecules tend to more H-bonds formation. This could be the possible reason for the high contribution of coulombic energy toward water/AWC interaction in system C.

Additionally, it is believed that there are plenty of hydroxyl groups in the interlayer of the AWC channel, which can form H-bonds with the water molecules in pores, therefore greatly influencing the water molecules’ orientation. Because the water molecules are strongly attracted by the magnesium ions in the interface, their mobility is restricted and results in a decrease in the extent of hydrogen bonding with the OH channel in system B. The results confirm that the transfer of water into pores of the channel wall depends on the less degree of hydration of the ion with the water molecules. In fact, by increasing the number of H-bonds between the water wire and the pores of the channel, the water flow into the AWC also increases during the simulation. Furthermore, the water flow inside the OH channel is significantly related to the pore radius, which leads to the formation of hydrogen bonds inside the pores. Accordingly, the formation of HBs in the water channels is very necessary for having high water flow in these systems. These findings revealed that the results of HBs are in good agreement with the water flux analysis.

The findings of this study indicated that the rejection of positively charged ions increases during the simulation process, and this phenomenon is mainly due to the surface charge of the membrane and an increased rejection through electrostatic repulsion. Therefore, during the permeability of water molecules inside the OH channel, the Ca2+ ions are away from the surface of the substrate. In fact, the Ca2+ is surrounded by H2O molecules meaning that the H2O could pack the Ca2+ ions in the outer pore of the channel and resulting in H-bond interaction between them. It is thought that the interaction of oxygen atoms of H2O molecules with the empty orbital of Ca2+ plays a leading role in the HBs interaction between these components.

Free energy calculations metadynamics

In order to explore the free energy landscape for the process of distribution of water molecules across the OH channel, different types of well-tempered metadynamics simulations are performed, such as Ca2+/AWC-Sol, Mg2+/AWC-Sol, NO3−/AWC-Sol, AWC-Sol and Ca2+- Mg2+- NO3−/AWC-Sol (co-existing) systems.

Figure 10 reveals the free energy surfaces (FES) of the transfer process for the individual center of mass (COM) of water molecules concerning the COM of the active sites in the AWC channel. For long distances of the water molecules from the AWC surface, the free energy set is to be zero, while it becomes more and more negative as the water molecules move toward the interior pores of the nanochannel via the transfer process. As seen in Fig. 10, the global minimum is reached in distances of d = 1.68, d = 1.93 nm with ~ −241.912 and ~−270.98 kJ mol−1 free energy in NO3− /AWC-Sol and Ca2+/AWC-Sol systems, respectively. However, the free energy of the global minimum collapsed to ~−200.47 at a longer distance of d1 = 5.13 nm in Mg2+/AWC–Sol system. Besides, in NO3−/AWC-Sol and Ca2+/AWC-Sol systems, in the process of reaching their respective global minimums, they experience local minimums of about -230 and −235, respectively, which are commonly presented as reaction coordination curves. To some extent, this feature is related to the small size of the hydrated Mg2+ ion that tends to attract the water molecules, and more water molecules are gattered to hydrate around it. Since the calcium ion has a slightly larger ionic radius than magnesium, it has lower hydration energy. Therefore, its adjacent water molecules interact more with the hydroxyl channel, and its FES becomes more negative. In the case of nitrate ions, these ions could slightly enter the cavity and also form the HBs with the hydroxy groups of AWC. Consequently, fewer water molecules are allowed to pass through the membrane and obtain a lower global minimum than in system C. In co-existing system, the landscape profile experienced the energy corresponding to the water transfer in the presence of the different ions such as Ca2+, Mg2+, and NO3−. The FES pattern of the co-existing system in Fig. 10 shows that the water molecules in the presence of different ions have the lowest free energy about ~−185.34 kJ mol−1 at a steady state. This phenomenon may be due to the very limited diffusion of different ions in the AWC framework. Free energy profile only for water molecules transported through the AWC channel in the absence of ions is also obtained, where the interaction exists between the permeated water molecules and AWC. An energy raising is observed in the local energy minima of the AWC/Sol system and the FES reached −289.305 kJ mol−1. This behavior can be explained by the formation of the hydrogen bonds between H2O and AWC, consisting of oxygen atoms from both the water molecules and the COOH groups at the edge of AWC monomers.

Fig. 10: The FES patterns.
figure 10

For transferring water molecules into the OH-Channel pores.

Full size image

The trajectory of well-tempered metadynamics simulations showed that there is no steric hindrance between water molecules and the monomers of the AWC channel. Furthermore, the hydrogen bond between the host and guest is caused that the water molecules being pulled down from the channel pores. It is worth mentioning that these results show a nearly perfect agreement with the results reported of interaction energies in Table 1.

Discussion

Therefore, it can be concluded that the classical molecular dynamics and well-tempered metadynamics simulations are done to gain molecular insight into the density distribution of water molecules across the AWC channel along with the removal of the ions. Our results predicted that the systematic design and flexibility of the channel, the effect of size of small ions, hydrogen bonds, and electrostatic interactions are the major factors in specifying the permeability of water molecules and ion rejection. The results of MD simulations showed that AWCs could provide paths for selective and rapid water permeation via the formation of water-wire networks. Moreover, the order of water permeability toward the OH channel is System C > System A > System B, which this behavior may be related to the size of the ions. Metadynamics simulations are also carried out for investigation of water transport in OH-channel and the possibility of ions removal. The obtained results revealed that the global minimum at FES is about ~−255.98 kJ mol−1 for system C, which is almost higher than the free energy values of both other systems. It is worthy to mention that the free energies landscape of Wt-metaD simulations has good agreement with the results of MD simulations that measured the permeability of water molecules and ions in the OH channel. In general, to design a suitable incoming water treatment system, the availability of active sites and also the nanopore’s size of the water channel should be considered to increase system efficacy.

Methods

MD simulations section

Herein we focused on AWC based on octyl-ureido-polyols, which are can capable of self-assembly into hydrophilic hydroxyl channels to selectively transport water with ion exclusion (Fig. 1). It is worthy to mention that the initial structure of the hypothetical OH-channel is taken from the X-ray data, which is reported by Barboiu et al.4. In this study, the self-assembly AWCs system based on octyl-ureido polyols for simulations is designed that include five layers and 1720 atoms to the removal of Mg2+, Ca2+, and NO3− ions and also monovalent ions such Na+ and Cl− ions.

The initial configurations containing the monomer of AWC and the water molecule are built with GaussView21 software and then optimized at the DFT level of theory (m062x/6–311G∗)22 via the Gaussian09 package program23. The location of the monomers of AWC and the water molecule are generated using the Packmol program24,25. The AWC simulation boxes are simulated with x, y, and z dimensions of 4 × 4 × 12 nm3, respectively, containing the AWC at the center, with the original 200 TIP3P water model on the left and right of the hydroxyl channels. Then ions and ethanol are placed on the right side of the simulated box. The simulation boxes are chosen to be sufficiently large to prevent any bias of the Periodic Boundary Conditions.

It should be noted that different water models have significantly different properties when simulated under the same conditions. A lot of research showed that the TIP3P water model gives faster dynamics when compared with the experimental values for liquid water21. Wang and coworkers confirm that the TIP3P water model still well predicts water transport properties26. In addition, Mark and Nilsson explored TIP3P water molecules moving faster than those of TIP4P and are also widely used for modeling bimolecular simulations27. The periodic boundary condition for the simulated systems is considered to forbid the interaction of components of their adjacent cells. The force field parameters for the components of the considered systems are obtained from the GROMOS 54a7 force field28. The ethanol solvent is applied to modulate the water transport permeability with ion excretion. All of the MD simulations are performed using the GROMACS29 Software Package (version 2019.2). Van der Waals interactions are truncated via a cutoff of 1.4 nm, and particle mesh Ewald (PME) method30 is applied for the long-range electrostatic interactions. The temperature and pressure are maintained at 310 K, and 1 atm during the simulation by the Nose-Hoover thermostat31 and the Parrinello–Rahman barostat32. The linear constraint solver (LINCS) algorithm33 with a 2 fs integration time step is used to constrain bond lengths in the simulation. Each of the three simulation systems is energy minimized via ∼10,000 steps of the steepest descent method to relax any steric conflicts before beginning the simulations. Then, two phases of equilibration, such as constant volume (NVT) and constant pressure (NPT) ensembles are subsequently carried out by 1.5 fs time steps. Finally, MD simulations of the whole system for 60 ns are performed. The simulations are visualized with the Visual Molecular Dynamics (VMD) program34. The details of the simulation boxes are presented in Table 2, and also for AWC/Na+ and AWC/Cl− systems are listed in Supplementary Table 1.

Table 2 Details of the simulation patterns.
Full size table

Metadynamics simulations

Well-tempered metadynamics (Wt-metaD) simulation developed by Parrinello and co-workers35 is an efficient method to detect the free energy surface as a function of the set of collective variables (CVs). Well-tempered metadynamics ensure a faster convergence in the long time limit compared to the standard metadynamics. The analysis of free energy surfaces (FES) for water transport in the AWC pores, along with the removal of ions, is carried out via the well-tempered metadynamics simulation. The sum_hills tool in Gromacs 201836, patched with the PLUMED version 2.5.2 plugin37, is used for the Metadynamics calculations. The initial Gaussian height and width are set to 1.0 kJ mol−1 and 0.25 Å, respectively, that deposited every 500 time steps with a bias factor of 15. Finally, it is worth mentioning that the metadynamics simulations are applied for 50 ns for all investigated systems. More details of the well-tempered metadynamics simulation are analyzed and presented in the “Results and discussion” section.