Introduction

The field of twist angle engineered moiré heterostructures has emerged as the latest platform to study strongly correlated quantum matter in condensed matter physics. Recent advances in graphene-based moiré systems have unveiled a vivid spectrum of correlation-driven unconventional phases. For example, in magic-angle twisted bilayer graphene (MATBLG), exotic phases and phenomena like superconductivity2,3,4,5,6,7,8, correlated-insulator4,8,9,10,11,12,13,14, Chern-insulator15,16,17,18, ferromagnetism19, Dirac revival14,20,21, and giant thermopower at low temperatures22,23 have been observed. Twisted double bilayer graphene (TDBLG) is another prominent member of graphene-based moiré heterostructures, where two sheets of Bernal-stacked bilayer graphene are stacked on top of each other with a small twist angle between them (Fig. 1a). The resultant reconstruction of electronic levels into bands in the moiré Brillouin zone (mBZ) leads to the formation of low energy bands, whose bandwidth is sensitive to the twist angle24,25,26. The bandwidth is minimum around an angle ~1. 2°. Unlike MATBLG, the flat bands in TDBLG survive over a broader range of twist angles (1. 1° − 1.35°), providing a robust foundation to study strong correlation effects27. The band structure of TDBLG can also be tuned by a perpendicular electric field28,29,30,31, which can drive the system from a metallic to an insulating state with interesting topological properties.

Fig. 1: Thermal and electrical transport in Twisted double bilayer graphene (TDBLG) at zero magnetic field.
figure 1

a Schematic of TDBLG with temperature gradient (TH and TC respectively are the hot and cold terminal temperatures). b Band dispersion of TDBLG with twist angle 1. 2° along the high symmetry axis in the moiré Brillouin zone (mBZ). The band structure shows an energy overlap (shaded region) of ~ 4.5 meV between valence (blue) and conduction (red) bands. c Density of states of the valence (blue) and conduction (red) bands as a function of normalised carrier density (n/ns), where n is the charge carrier density induced by the gate voltage and ns is the carrier density required to fulfill the flat band. The shaded region indicates the presence of band overlap. d Resistance (R) versus carrier density (n) as function of increasing temperature. Several resistance peaks can be observed at full-filling of band and near the charge neutrality point (CNP). The shaded region indicates the presence of band overlap. e Evolution of thermopower as a function of normalized density n/ns at several temperatures.

Full size image

Theoretical predictions have shown that in TDBLG the low energy valence and conduction bands, though separated in momentum space, overlap in energy, allowing the co-existence of electron-hole pockets near the CNP24,25,26. The co-existence of electron-hole pockets has fascinating implications like colossal magnetoresistance32, large non-saturating thermopower with applied magnetic field33 (these are also seen in Dirac and Weyl semimetals33,34,35,36,37). A similarly enhanced magnetoresistance ( ~ 200%) has been reported for semimetallic bismuth and graphite38,39. However, experimental demonstration of compensated semimetallic phase or the co-existence of electron and hole pockets in TDBLG has not been reported earlier. Electronic interactions in compensated semimetals can lead to formation of excitonic insulator40,41 driven by Coulomb attraction between the electrons and holes, or to exciton condensation in metallic42,43,44 backgrounds near the CNP1. Experimentally, the effects of strong electronic correlations in TDBLG have been seen when the samples are subjected to strong perpendicular electric fields28,29,30,31 or magnetic fields27 at the commensurate fillings of moiré superlattice. However, without these perturbations, TDBLG has shown29,45 trivial metallic behaviour without any report of strong electronic correlations at CNP.

This work presents a comprehensive study of temperature, carrier density and magnetic field-dependent resistance, and thermopower of TDBLG with a twist angle 1. 2°. At zero magnetic field, the thermopower is almost zero around the CNP due to compensation from opposite charge carriers (electrons and holes). Upon application of a small magnetic field, the thermopower at low temperatures ( < 3K) increases rapidly till 100 − 400 times before saturating to 10 − 15 μV/K within ~ 0.25 T. Similarly, the magnetoresistance (MR) at the CNP increases quite rapidly with the application of a small magnetic field and saturates before 1T with an enhancement of 2500%. The enhancement of thermopower by two orders of magnitude and large MR at the CNP of TDBLG is quite striking and is not seen for MATBLG in our study. A two-band particle-hole asymmetric model of TDBLG band structure with the co-existence of electron and hole pockets24,25,26 is invoked to qualitatively and semi-quantitatively explain the results. The compensated semimetal allows a quantum transport regime with small Hall angles36,38, where the electric current is dominated by Drude dissipative processes; however, the thermal current is dominated by the spiraling of the charge carriers in crossed electric and magnetic fields. These two different mechanisms lead to a strong enhancement of thermopower and magnetoresistance. We note that our data provide the first clinching evidence for compensated semimetallic phase near the CNP in TDBLG.

Further, the metallic behaviour (resistance decreasing with decreasing temperature) around the compensated semimetallic phase is quite striking. Near the CNP, we find an unusual sublinear temperature dependence of the resistance (R ~ Tα, α ~ 0.67 − 0.83) below 10K, whereas the temperature dependence is superlinear (R ~ Tα, α ~ 2 − 2.5) away from the region of co-existing electron-hole pockets on either side of CNP. Note that the temperature dependence of the resistance becomes linear around the CNP above 10K. Here, we invoke the recent theory of excitonic metal1 at the CNP of TDBLG to explain our unusual temperature dependence of the resistance.

Results and Discussion

Device and setup

The TDBLG device is realized by following the tear and stack technique2. Two AB-stacked bilayer graphene sheets are stacked with a relative twist angle (1. 2°) and encapsulated by hexagonal boron nitride (hBN). The details of the device fabrication and measurement setup are mentioned in the supplementary information (Supplementary Note 1). For the two-probe resistance measurement, the standard lock-in technique (13 Hz) with current bias has been used. For the thermopower measurement, an isolated gold line is placed parallel to our device, serving as a heater. Passing a current through the heater creates the temperature gradient across the device (Fig. 1a shows the temperature profile as a color gradient). The generated thermometric voltage across the device is measured using standard V2ω technique46,47,48,49,50,51,52. For the temperature gradient, we have employed Johnson noise thermometry for the precise measurement of ΔT, which gives an accurate value of Seebeck coefficient, S = V2ω/ΔT. The noise measurement is elaborated in our previous work22 and shown in the supplementary information (Supplementary Note 2–6). All the measurements are performed in the linear regime (see Supplementary Note 7). We note that for accurate measurement of the ΔT, a linear fall-off of the temperature is necessary. Purposefully a simple two-probe geometry is implemented instead of having multiple metal leads (that can act as constant temperature heat sinks) which would have heavily altered the linear temperature fall-off to a more complicated form. We have solved Fourier heat diffusion equations for a multi-layer stack using finite element calculations in Comsol (Supplementary Note 14) to validate our assumption of a linear temperature profile for a two-probe geometry.

Electrical and Thermal Transport

Carrier density-dependent resistance measured at several temperatures (between 20 mK − 40 K), is shown in Fig. 1d. The carrier density, n, is obtained from the gate voltage applied to the Si/SiO2 back gate by assuming an effective capacitance of the device. At low temperature, the resistance shows two strong peaks at large positive and negative densities of Fig. 1d with associated insulating behaviour (resistance increasing with decreasing temperature). We identify these peaks with the occurrence of moiré gaps, i.e. with carrier densities n = ± ns, where the moiré conduction (valence) band of TDBLG is completely filled (emptied out). This corresponds to having 4 electrons (holes) per moiré unit cell. Using the expression2,9\({n}_{s}=\frac{4}{A}\approx \frac{8{\theta }^{2}}{\sqrt{3}{a}^{2}}\), where A is the area of the moiré unit cell and a is the graphene lattice constant; this translates to a twist angle of θ ≃ 1. 2°. This confirms that the twist angle is within the range of observable flat bands for TDBLG.29,30,53.

The resistance exhibits metallic behaviour at all densities other than the vicinity of the moiré insulator, including at the CNP. This is consistent with earlier work on magic angle TDBLG27,30,31 and is in stark contrast with MATBLG, which behaves like an insulator4,5,9 near the CNP. Theoretically, this is explained by the fact that MATBLG shows protected Dirac nodes with zero density of electronic states at the Fermi level54, while the valence and conduction bands of magic angle TDBLG overlap in energy24,25,26, leading to formation of a compensated semimetal at the CNP with electron and hole pockets. The overlap of the valence (blue) and the conduction (red) bands of TDBLG can be seen from the theoretical band dispersions of TDBLG (Fig. 1b), calculated at a twist angle of 1. 2°. A detailed model of the moiré bands, which breaks particle-hole symmetry and includes trigonal warping, is needed to obtain this energy overlap of ~ 4.5 meV between the bands (see Supplementary Note 10). Figure 1c shows the variation of the density of states (DOS) at the Fermi level with the carrier density n (separately for these two bands). The electron and hole pockets co-exist between carrier densities n− ~ − 0.7 × 1012 cm−2 (n−/ns ~ − 0.2) and n+ ~ + 0.4 × 1012 cm−2 (n+/ns ~ 0.12). This density span is marked by grey shaded region in Fig. 1c–e. The resistance at a fixed temperature shows additional peaks/dips as a function of density visible between the CNP and the moiré insulator. These features survive up to ~ 20K and become more prominent with increasing temperature. However, these features do not appear exactly at commensurate fillings and are not caused by strong electronic correlations; rather, they may be correlated with Van-Hove singularities crossing the Fermi level and are consistent with the reported results on TDBLG27.

The thermopower or Seebeck coefficient is defined as a generation of electric voltage due to a temperature difference (\(S=-\frac{\Delta V}{\Delta T}\)). Alternatively, using Onsager relation, S can be written in terms of the Peltier coefficient (the ratio of heat current, JQ produced by an applied electrical current, Je) as: \(S=\frac{1}{T}\frac{{J}_{Q}}{{J}_{e}}\). At the CNP or in compensated semimetals, the heat carried by the opposite charge carriers flows in opposite directions. Thus at a given applied current, S will be very small and proportional to: \(\frac{{J}_{Q}}{{J}_{e}} \sim \frac{({n}_{e}-{n}_{h})}{({n}_{e}+{n}_{h})}\). Here, ne and nh are the carrier concentrations for electron and hole, respectively. The density-dependence of thermopower at different temperatures from 1K to 5K is shown in Fig. 1e. As expected, S reverses sign at the CNP as well as at n = ± ns. We also observe several interesting features in the density dependence of thermopower away from CNP. These include additional change of sign at n/ns ~ + 0.3, − 0.4, dips around n/ns ~ ± 0.75 and peaks in between. A comparison between measured S and thermopower predicted by Mott formula has been discussed in the supplementary information (Supplementary Note 15). The sign change is related to change of topology of the Fermi surface (from electron (hole) like to a hole (electron) like) while peaks and dips may be related to possible Lifshitz transitions. However, in this article, we focus on transport near CNP, leaving the explanation of these features for future work.

Thermopower enhancement with low-magnetic field

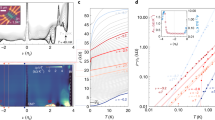
The metallic resistivity, together with the sign change of thermopower at CNP, strongly suggests that the system is a semimetal. However, electrons and holes have opposite charges and respond to magnetic fields in different ways. Hence, for clear evidence of ambipolar transport, we now consider thermal transport in our sample in the presence of a magnetic field B applied perpendicular to the plane of the sample. Figure 2a shows the variation of the measured S with B for three values of doping near CNP at 1K. S is almost zero around the CNP in the absence of magnetic fields; it increases rapidly with the application of few milli-Tesla (mT) magnetic field and saturates around ~ 10 − 14 μV/K beyond 0.3T. The 2D-colour plot in Fig. 2c shows this large enhancement of thermopower restricted to the vicinity of the CNP.

Fig. 2: Finite magnetic field thermopower and resistance measurements.
figure 2

a Magnetic field dependence of measured thermopower at n/ns = + 0.03, − 0.002, − 0.03 at 1K, where ns is the carrier density (n) at full filling of the flat band. The inset shows the theoretically predicted thermopower for compensated semimetallic band. b Theoretically extracted normalized effective charge density (\(\frac{({n}_{e}-{n}_{h})}{({n}_{e}+{n}_{h})}\)) (ne(nh) being the electron(hole) density) as a function of n/ns. c 2D color plot of thermopower as a function of perpendicular magnetic field and n/ns at 1K. (d) Cartoon illustration of the (Etot × B) drift on the carriers in the limit when magnetic field (B) approaches BH (i.e at magnetic field where Hall angle θH → 90o). The Hall voltage along the y direction leads to an electric field EH, where ∣EH∣ ≫ ∣Ex∣ (Ex is the applied electric field) in the limit θH ≈ 90o. Electrons (labeled e) and holes (labeled h) both drift alongside in presence of crossed electric (Etot = Ex + EH ≈ EH) and magnetic field contributing additively to the heat current36. e 2D color plot of thermopower plotted over a wide range of density / n/ns (bottom axis / top axis) and magnetic field (divided by flux quanta Φ0) with red (yellow) dashed lines marking the landau levels emanating from n/ns = 0 ( − 1). f Resistance as a function of perpendicular magnetic field and n/ns at 20 mK. g Perpendicular magnetic field dependence of measured resistance at several n/ns at 1 K. The presence of semimetallic band is further reflected through metal-insulator transition of resistance versus temperature curve with increasing perpendicular magnetic field, as demonstrated in the inset.

Full size image

The enhancement of S at relatively low-magnetic fields for compensated semimetals can be understood in the following way, which has been quantitatively explained by Feng et. al36. In presence of crossed electric (E) and magnetic (B) fields, the drift velocity of charged particles have two components: a Drude response, \({v}_{d}=\pm \frac{\mu E}{1+{(\mu B)}^{2}}\) (μ being the mobility of electrons and holes) and a E × B spiralling component (shown in Fig. 2d). For the electric current, the Drude response is proportional to nT = ne + nh, while the response from the spiral component is proportional to Δn = ne − nh, where ne and nh are electron and hole densities. Note that Δn = ne − nh is the effective charge carrier density of the device as defined as n earlier. Since Δn ≪ nT, one can have a situation where the transport is in the quantum regime36 (μB ≫ 1) for B > B1 (B1 ≈ 1/μ), but the Hall angle \(\tan {\theta }_{H}=\frac{{\sigma }_{xy}}{{\sigma }_{xx}}=\mu B\Delta n/{n}_{T}\) is still small due to the compensation from the ratio of densities; i.e. the electric transport is dominated by the Drude response. However, for the thermal current, the Drude response is proportional to Δn, while the response from the spiral component is proportional to nT, and hence thermal transport is dominated by the drift coming from the spiral component. In this regime, the thermopower Sxx = JQ/TJe is given by \({S}_{xx} \sim \frac{{k}_{B}^{2}T}{e{\epsilon }_{F}}\frac{\Delta n}{{n}_{T}}{\mu }^{2}{B}^{2}\). This rapid quadratic rise of the thermopower is seen in our data in Fig. 2a. At higher magnetic fields B > BH (\({B}_{H}\approx {B}_{1}\frac{{n}_{T}}{\Delta n}\)), where μB ≫ nT/Δn, one enters the regime of extreme quantum transport with large Hall angles, where the electric current is also dominated by the drift coming from the spiral component. In this case, the thermopower saturates and is given by \({S}_{xx} \sim \frac{{k}_{B}^{2}T}{e{\epsilon }_{F}}\frac{{n}_{T}}{\Delta n}\). The inset of Fig. 2a shows the theoretically calculated (mentioned in Supplementary Note 11) thermopower for compensated semimetallic band36, which resembles very well with our experimental data. In Fig. 2b, we plot \(\vert \frac{\Delta n}{{n}_{T}}\vert\), obtained from theoretical band dispersions, as a function of the carrier density. We find that this theoretical \(\vert \frac{\Delta n}{{n}_{T}}\vert\) falls to zero (ne ≈ nh, hence Δn = ne − nh → 0) in the region where the large saturation value of thermopower is seen, corresponding to the region of co-existence of both the electrons and holes. Outside this region, the theoretical \(\vert \frac{\Delta n}{{n}_{T}}\vert\) remain close to 1, and thus no enhancement of thermopower is expected as seen in the experimental data (Fig. 2c). It should be noted the enhanced thermopower should change its sign around the CNP. However, as can be seen in Fig. 2c, the sign change happens around n/ns ~ + 0.05. This discrepancy may arise due to differences in mobility for electrons and holes, which was assumed to be the same in the simple model36 as described before. Also, note that for n/ns > + 0.05, the enhancement is negative but with a smaller saturation value. In Fig. 2c we observe a distinct region near CNP (particularly spanning more in the hole side) where quantum oscillations in S are suppressed. While away from this region (both in electron and hole-doped regions) clear Landau fans can be observed. This suggests the apparent suppression may be connected to the co-existence of electron-hole pockets. One possible reason may be, that the slightly mismatched effective mass of either carrier can form landau levels (L.L) with marginally different L.L gaps. This small misalignment in energy gives rise to effective L.L energy gaps much smaller than L.Ls of either carrier, hence the oscillations are smeared out.

Although the enhancement of thermopower for semimetals like bismuth38,55 and tantalum phosphide56 in the bulk form have been reported earlier, the predicted saturation of thermopower with the magnetic field previously has not been observed experimentally. Our work on TDBLG provides the first experimental evidence of the saturation of thermopower for compensated semimetals accurately; we also demonstrate the tunability of the thermopower with carrier concentration because of the two-dimensional nature of our system. Additionally, for comparison we have studied the thermopower response for MATBLG with the magnetic field, and it barely changes around the CNP (Supplementary Note 8), as expected for non-compensated semimetals. It should be noted that the enhancement decreases as we increase the temperature and vanishes beyond 10K (Supplementary Note 9) where quantum effects are destroyed due to increased scattering rate and the idea μB ≫ 1 is no longer valid.

We also have measured the thermopower over a wider range of filling and magnetic field (at 1K) as shown in Fig. 2e. Alongside the previously mentioned thermopower enhancement around CNP we also observe clear signatures of Landau fans emanating from n/ns = 0, − 1. Using the Diophantine equation57 for Landau levels (L.L) we find a two-fold degenerate L.L sequence at both fillings at high magnetic fields. We observe a further decrement in thermopower to occur beyond 2T. At these higher values of the applied perpendicular magnetic field, symmetry breaking causes a gap opening at CNP. The lack of DOS (due to gap opening) causes decay in thermopower with any further increase in a magnetic field. At even higher fields, Landau levels start emerging resulting in oscillations in thermopower along the crossings of the Landau fans.

Large magnetoresistance at CNP

To further investigate the distinct footprints of electron-hole pockets in TDBLG, we examine the magnetoresistance (MR) of the system and its temperature dependence near the compensated region. In Fig. 2f a large enhancement of MR (measured at 1K) confined within the vicinity of CNP can be observed in the 2D-colour plot of R as a function of B and n/ns. Figure 2g shows resistance (measured at 20 mK) as a function of the magnetic field at different carrier densities. Close to CNP, the MR monotonically increases with B and saturates around a magnetic field of 1T with a maximum increment of 2500%. The rapid rise of the MR with a magnetic field can be understood from the quantum limit of electrical transport33,58, where it is still dominated by the Drude response, while the saturation behaviour is dominated by the spiral component of current. Similar to thermopower, the maxima of MR appears slightly away from the CNP at n/ns ~ + 0.05 (see Fig. 2f). This could also be due to the mobility mismatch between electrons and holes. Note that the position of the CNP was identified by looking at the resistance peak in Fig. 1d, the thermopower crossing point at zero magnetic field in Fig. 1e, and the Landau Fan emerging point in Fig. 2e.

The high MR and the saturation is a distinctive behaviour of many compensated semimetals38,59. Normal metals, on the other hand, have higher scattering rates which limit their magnetoresistance. The temperature dependence of resistance at various magnetic fields at a fixed density near the charge neutrality is shown in the inset of Fig. 2g. The behaviour is very similar to that of previously reported compensated semimetals38,39,60. We can clearly see that the system exhibits a field-induced metal-to-insulator transition around a magnetic field of 0.2T.

Sublinear temperature scaling of resistance around CNP

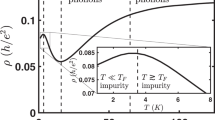
As seen in Fig. 1d, we observe a monotonic increment of resistance with temperature in the whole density range, suggesting metallic transport throughout the flat band. In Fig. 3a, we study the temperature dependence of the resistance of the sample at several densities on either side of CNP. At large positive or negative densities, when there is only one type of carrier, we see that the resistance has a superlinear (with exponent between 2 and 2.5) behaviour with a temperature below 10K (marked by blue solid line). However, the situation changes dramatically near CNP, where both carriers are present. The resistance at these densities (n/ns = − 0.051,   − 0.021,  0.00,  0.02) show a sublinear behaviour with temperature in the range 200 mK − 10 K marked by blue solid line, and a linear dependence above 10 K. The sublinear dependence can be fitted using R = aTα + R0 (where a, α and R0, respectively are the proportionality constant, exponent and zero temperature resistance), and obtain α between 0.67 − 0.83. The insets show the low temperature regime (blue fitting) in a log-log scale to better represent the low-temperature behaviour. The evolution of α with n/ns is shown in Fig. 3b (in blue circles with error-bar). It can be noticed from Fig. 3b that the sublinear temperature dependence is prominent in the region where the electron and hole pockets co-exist, which is marked by the vertical dashed lines in Fig. 3b. As described before, in this measurement scheme (optimized for thermopower) we are limited to two-terminal resistance measurements, which has finite contributions from the contact resistance. It should be noted that beyond the full-filling in Fig. 1d, the resistance barely changes with increasing temperature, where as within the full-filling the resistance increase monotonically (metal-like) with increasing temperature (Figs. 3a and 1d) and changes by ~ 200Ω/Kelvin. This suggests that the contact resistance at the measured low temperature range (200 mK − 10 K) barely changes, and our data is predominantly governed by the channel resistance.

Fig. 3: Electronic correlations in Twisted double bilayer graphene (TDBLG) near charge neutrality point (CNP).
figure 3

a Power-law fitting of resistance as a function of temperature at different densities. Away from the CNP, at normalized carrier densities n/ns ~ − 0.150, − 0.100, 0.095, the best fit for R = R0 + aTα (R0, a and α respectively are the zero temperature resistance, proportionality constant and exponent) is shown as the blue (red) line at low temperature (high temperature) range. The low temperature exponent shows a clear superlinear behaviour. In contrast near CNP, at n/ns ~ − 0.05, − 0.02, 0.0, 0.02, the resistance shows a sublinear behaviour (blue line is the fit) at low temperature (0.02 − 10 K). The insets show the data in log-log scale. The behaviour of R above 10 K at all density ranges is almost linear with T. b Fitted exponent (α) both for low temperature (<10K) and higher temperature fitting ( > 10K and < 40K) depicted by black circles (with blue error bars) and red circles (with grey error bars) respectively, the error bar represents 95% confidence bound of the fitting for cofficient α, the blue vertical dashed lines frame the region of electron and hole co-existence. The low temperature exponent shows nontrivial sublinearity inside the aforementioned co-existence. c Calculated Fermi surfaces in TDBLG at CNP showing the electron (blue) and the hole (red) pockets. Note that the centres of the pockets are shifted in momentum space (Q1, Q2 and Q3 being the respective shifts). (d) Schematic representation of indirect excitons as pairing between electrons and holes with momentum offset Q0.

Full size image

The observed sublinear temperature dependence of the resistance around the CNP in Fig. 3a and b is quite unusual. Note that in graphene61 and MATBLG4,62, one finds insulating behaviour near the CNP due to vanishing density of states. In contrast, small electron and hole pockets are formed in TDBLG near CNP, (see Fig. 3c) which leads to metallic behaviour. However one would expect a T2 behaviour of resistance at the lowest temperatures and a linear temperature dependence above Bloch Gruneissen temperature, which is within a few Kelvin in TDBLG near CNP. Indeed, we find linear dependence of resistivity for T > 10K. Though, beyond n/ns = ± 0.2 the fitting tends to move marginally away from the expected linearity as seen in Fig. 3b. It should be noted that, beyond n/ns = ± 0.2 the Fermi surface increases resulting in higher Bloch Gruneissen temperature, as a result to see the expected linearity one may need to go higher temperature than the measured temperature range. To understand the sublinear dependence around the CNP, we rely on the recent theory1, which predicts the formation of excitonic condensate due to Coulomb attraction between the electron and hole pockets (see Supplementary Note 12, 13). Since the electron and hole pockets are shifted in momentum (see Fig. 3c), indirect excitons with momenta connecting the center of the pockets are formed, as shown in Fig. 3d. This leads to an excitonic metal at low temperatures. The fermions in this metal are scattered by Landau-damped critical fluctations of the excitonic order. This leads to a non-Fermi liquid behaviour1,63,64,65,66,67, where the scattering rate and hence the resistance, R ~ T2/3. Note that the hole pocket, when shifted by the momentum of the exciton, lies on top of the electron pocket and hence this is similar to the scenario for an order parameter with zero momentum63, which is known to lead to T2/3 scaling of scattering rates1. Based on the theory, we believe that our experimental data with sublinear temperature dependence of the resistance with exponent 0.67 − 0.83 around the CNP shows the signature of excitonic metal in TDBLG.

Conclusions

We have reported strong enhancement of thermopower and magnetoresistance in TDBLG at low temperatures near the CNP for relatively modest magnetic fields. This behaviour is understood in terms of electric and heat transport in a compensated semimetal and provides clear evidence of simultaneous electron and hole pockets in this system. The resistance at low temperatures shows a sublinear dependence, attributed to the formation of an excitonic metal described in recent theoretical work1. Note that the presence of disorders around the CNP can not explain the simultaneous observation of large metallicity (~200 Ω/Kelvin), orders of magnitude of enhancement of thermopower, magneto resistance, as well as quantum oscillations observed with a few hundred mT of the magnetic field. It will be interesting to see how these features evolve with a perpendicular displacement field, which is left for future studies.

Methods

Device fabrication and measurement setup

For assembling the hBN encapsulated TDBLG, we have used the standard ‘tear and stack’ technique2,9. The encapsulated device is placed on a Si/SiO2 substrate acting as an electrostatic gate. The fabrication process is explained in much greater details in supplementary information (Supplementary Note 1). The length and width of the representative device are approximately 6 μm and 3 μm, respectively. An optical image of the measured device is provided in SI-Fig. 3. An isolated thin gold line, placed ~ 3 μm away from the source probe acts as a heater. During thermopower measurement, upon injecting a current (Iω) in the heater line a temperature gradient arise across the length of the device. The source contact neighbouring the heater gets hotter (Th) while the drain is maintained at constant bath temperature of the mixing chamber (m.c) plate due to cold ground. The voltage (V2ω) generated across the channel is measured using standard Lock-in amplifier (Supplementary Note 2). For resistance measurement low-frequency ( ~ 13 Hz) Lock-in technique (Supplementary Note 2) is employed. To measure the temperature difference (ΔT), we employ Johnson noise thermometry. The noise thermometry circuit consists of LC resonant (fr ~ 720 kHz) tank circuit, followed by a cryogenic amplifier and a room temperature amplifier (see SI-Fig. 2d). A detailed gain calculation of the amplifier chain is mentioned in the supplementary information (Supplementary Note 8). As depicted in SI-Fig. 2a a relay situated on the mixing chamber plate is used to switch between high-frequency (ΔT) and low-frequency (Resistance and V2ω) measurement scheme.

Theory

Twisted Double Bilayer Graphene consists of two Bernal stacked (AB) bilayer graphene (BLG) sheets with a relative twist angle θ between them. Here, we work with the ABAB stacking, so that the B sublattice of the top interface layer sits on top of the A sublattice of the bottom interface layer. Here we consider the band structure of TDBLG following Ref.s24,26. The details of the Hamiltonian construction can be found in the supplementary information (Supplementary Note 10). For this work, we have taken the following coupling parameters24, ℏv0/a = 2.1354 eV (the nearest neighbour tunneling amplitude along the monolayer graphene sheet), γ1 = 400 meV (the c-axis inter-layer hopping between the dimer sites), γ3 = 320 meV (the inter-layer hopping between the nondimer sites), γ4 = 44 meV (the coupling between dimer and non-dimer sites), and \({\Delta }^{{\prime} }=50\,\,{{\mbox{meV}}}\) (the potential difference between dimerized and non-dimerized sites). For the AA/BB and AB tunneling amplitudes across the twisted layers, we have used24, u = 79.7 meV and \({u}^{{\prime} }=97.5\,\,{{\mbox{meV}}}\) respectively in our calculations. In this work, we have taken a 184 dimensional matrix which gives an error of < 1% in the band dispersions at the magic angle of 1. 2°.

The Coulomb attraction between the electron and hole pockets lead to formation of indirect exciton condensates in TDBLG near CNP. In this calculation we will replace the Coulomb potential between electrons and holes by a screened short range potential. In fact we will use an effective momentum independent potential with the energy scale V0 ~ 10.8 meV. Note that there are three electron pockets separated from the three hole pockets by wavevectors Q1(2)(3). The mean field Hamiltonian describing the excitonic condensate is given by

$${{{{{{{\mathcal{H}}}}}}}}({{{{{{{{\bf{Q}}}}}}}}}_{i})=\left[\begin{array}{cc}\frac{1}{3}{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{c}-\mu &\Delta \\ \Delta &\frac{1}{3}{\epsilon }_{{{{{{{{\bf{k}}}}}}}}+{{{{{{{{\bf{Q}}}}}}}}}_{i}}^{v}-\mu \end{array}\right]$$
(1)

where, the \({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{c(v)}\) represents the non-interacting conduction (valence) band dispersion and the chemical potential is denoted as μ. Note the order parameter Δ is same for all the pockets and is determined self-consistently. We can then write the modified quasi-particle dispersion relation in presence of the excitonic condensate,

$${E}_{{{{{{{{{\bf{Q}}}}}}}}}_{i}}^{\pm }(k)=\frac{{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{c}+{\epsilon }_{{{{{{{{\bf{k}}}}}}}}+{{{{{{{{\bf{Q}}}}}}}}}_{i}}^{v}}{6}-\mu \pm \sqrt{\frac{{\big({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{c}-{\epsilon }_{{{{{{{{\bf{k}}}}}}}}+{{{{{{{{\bf{Q}}}}}}}}}_{i}}^{v}\big)}^{2}}{36}+{\Delta }^{2}}$$
(2)

The above energy spectrum generates a finite Fermi surface near CNP, which leads to metallic transport in presence of the condensate.