Abstract
The characterization of a quantum device is a crucial step in the development of quantum experiments. This is accomplished via Quantum Process Tomography, which combines the outcomes of different projective measurements to deliver a possible reconstruction of the underlying process. The tomography is typically performed by processing an overcomplete set of measurements and extracting the process matrix from maximum-likelihood estimation. Here, we introduce Fourier Quantum Process Tomography, a technique which requires a reduced number of measurements, and benchmark its performance against the standard maximum-likelihood approach. Fourier Quantum Process Tomography is based on measuring probability distributions in two conjugate spaces for different state preparations and projections. Exploiting the concept of phase retrieval, our scheme achieves a complete and robust characterization of the setup by processing a near-minimal set of measurements. We experimentally test the technique on different space-dependent polarization transformations, reporting average fidelities higher than 90% and significant computational advantage.
Similar content being viewed by others
Introduction
The functionalities of a black-box quantum device can be assessed via Quantum Process Tomography (QPT) techniques. These techniques prescribe a set of experimental measurements to identify the unknown parameters of the underlying process matrix1. QPT is routinely performed across various quantum architectures, ranging from nuclear magnetic resonances2 to cold atoms3, trapped ions4,5, superconducting circuits6,7 and photonic setups8,9,10,11,12,13,14,15,16,17,18.
In principle, one could extract the analytical relations between the operator parameters and the outcomes of suitable projective measurements19. However, this proves to be often incompatible with realistic experimental noise, typically yielding nonphysical reconstructions. This inconvenience can be overcome by formulating the process tomography as an optimization problem, as first proposed for the tomography of quantum states20.
In this framework, the most elementary scenario is the characterization of an SU(2) gate \(\hat{U}\) acting on a two-level quantum system (qubit). Polarization of photons provides a natural way of encoding qubits, with \(\hat{U}\) implemented via one or multiple birefringent waveplates. Accordingly, the characterization of devices acting on light polarization can be accomplished via QPT21.
Here, we address the more challenging scenario of characterizing optical SU(2) gates that are dependent on some d-dimensional degree of freedom, hereafter referred to as lattice. We introduce a technique, named Fourier Quantum Process Tomography (FQPT), that allows retrieving all the parameters of the unknown transformation by processing only three sets of projective measurements collected in 2 conjugate planes. This method applies to SU(2 × d) transformations, which can be decomposed in a 2 × 2 block-diagonal form.
FQPT is validated experimentally on complex polarization transformations realized via liquid-crystal metasurfaces (LCMSs) patterned with high spatial frequencies22, and its performance is compared with a standard maximum-likelihood (ML) approach. In this experiment, the measurements can be conveniently chosen to be performed in two conjugate planes, namely the near and far field, wherein the light distributions are directly connected via a Fourier transform. If the near field is associated with an intermediate plane or two intermediate planes are selected, then the Fourier transform is replaced by a paraxial Fresnel propagator23. FQPT can also be implemented in other platforms. For instance, integrated photonic technologies24 can support additional chips specifically implementing the Quantum Fourier Transform (QFT) algorithm25,26,27. At the same time, SU(2) operations could be implemented either in the polarization28,29,30 or path encoding. In the latter case, the waveguide array would simulate a composite lattice. Similar schemes have also been reported in several non-photonic platforms31,32,33.
Results
Theory
A qubit rotation of an angle 2E around the axis n = (n1, n2, n3), with 0 ≤ E < π and ∣n∣ = 1, is described by an SU(2) operator:
where σ0 is the 2 × 2 identity matrix and σ = (σ1, σ2, σ3) is the vector of the three Pauli matrices.
The characterization of an optical SU(2) gate is typically performed by processing an overcomplete set of 16 projective measurements of the form:
where \(\left\vert a\right\rangle\) and \(\left\vert b\right\rangle\) are extracted from the three sets of states forming the mutually unbiased bases (MUB) of SU(2)1,8,10. The process tomography of the gate is then accomplished via an ML approach, i.e., by minimizing a cost function expressing the distance between the experimental outcomes \({I}_{ab}^{\exp }\) and the corresponding theoretical predictions \({I}_{ab}^{{{{\rm{th}}}}}\)10,21. Assuming Gaussian statistics, ML is equivalent to minimizing the cost function given by the mean squared error20:
This approach may become unfavorably time-consuming and less accurate in the case of transformations acting on high-dimensional Hilbert spaces. Here, we consider the case of unitaries, which depend on some additional parameter, e.g., a spatial variable or a lattice position. More precisely, we assume the parameters E, n1, n2, n3 to be functions of r, where r can be any set of either discrete or continuous variables. In this current study, we assume position r as a continuous variable. However, the discrete case can be obtained by replacing integrals with summations, i.e., ∫ f(x) dx → ∑x f(x).
The unknown unitary process acts on quantum states whose Hilbert space is the tensor product of a qubit space \({{{{\mathcal{H}}}}}_{i}\), associated with an internal degree of freedom, and a high-dimensional space \({{{{\mathcal{H}}}}}_{r}\), associated with the lattice.
We consider an input state uniformly distributed along r, with an internal state prepared as one of the MUB states \(\left\vert a\right\rangle\). \(\left\vert a\right\rangle\) is assumed to be the positive eigenvector of σ1, σ2 or σ3. The unknown unitary U(r) acts on this state, and then a projection onto the same internal state is performed. The probability distribution along r is \({{I}_{aa}({{{\bf{r}}}}) = | \langle a| U({{{\bf{r}}}})| a\rangle | }^{2}\). Reconstructing the unitary requires also knowing the phase of 〈a∣U(r)∣a〉. This can be done via interferometric measurements or phase retrieval techniques. Here, we focus on the second approach, since it can be easily implemented in a large variety of platforms. To this end, another measurement is performed to retrieve the probability distribution \({\tilde{I}}_{aa}({{{\bf{k}}}})\) in the reciprocal space of r. This is enabled by a QFT of the final state:
The choice of the Fourier basis is particularly convenient, as one can extract the wave function phase in each plane from the two probability distributions by applying phase retrieval techniques. Indeed, these rely on the existence of a unique phase distribution compatible with measured amplitudes in two conjugate spaces (up to global phase shifts). We specifically employed the Gerchberg-Saxton (GS) algorithm34. In particular, we can retrieve the amplitude \({A}_{a}({{{\bf{r}}}})=\sqrt{{I}_{aa}({{{\bf{r}}}})}\) and the phase \({\alpha }_{a}({{{\bf{r}}}})=\arg (\langle a| U({{{\bf{r}}}})| a\rangle )\). However, the latter is determined up to an unknown constant ξa. The amplitude and phase are related to the process parameters according to:
where a = 1, 2, 3, depending on which Pauli matrix is considered \(({\sigma }_{a}\left\vert a\right\rangle =\left\vert a\right\rangle )\). Thus, we obtain:
Equations (6a) and (6b) show that the extracted parameters depend on the global phase shifts ξa, which cannot be estimated from the phase retrieval method. Indeed, any phase that differs from αa(r) by a constant global shift yields the same measured amplitude in the direct and reciprocal space. Considering the ambiguity due to the global phase shift, we list all the possible energy modulations compatible with the measurements. In practice, we select N values of the global phase shift ξa,j = 2πj/N, with j = 0, 1, ... , N − 1. We specifically set N = 64. Only one of the candidates can best describe the process under investigation. To find it, we perform an additional measurement in the reciprocal space, obtained by evolving any input state without projection on the internal degree of freedom, e.g.:
where \(\left\vert b\right\rangle\) can be chosen arbitrarily, and ∥…∥ represents the norm of the transformed state. Crucially, this last measurement also provides the normalization factor for all the data. In this way, by numerically simulating the far field obtained from each of the N possible SU(2) evolutions, we can isolate the realization associated with the physical setup by sifting the one that minimizes the distance with the measurement of Eq. (7). This step, besides representing a computational bottleneck of the present method, does not affect its scalability.
We finally remark that, in principle, the method also works with only 2 sets of measurements. For instance, one could process I11(r) and I22(r), together with \({\tilde{I}}_{11}({{{\bf{k}}}})\) and \({\tilde{I}}_{22}({{{\bf{k}}}})\), to retrieve n1(r) and n2(r). In this case, the third component could be directly computed from the normalization condition: \({n}_{3}=\pm \sqrt{1-{n}_{1}^{2}-{n}_{2}^{2}}\). Combined with the final measurement in the reciprocal space, these add up to a minimal set of 5 total measurements, in perfect agreement with the argument provided in ref. 18. However, we observed that experimental noise may yield nonphysical results, i.e., n3 features a non-zero imaginary part at some location. This suggested integrating the minimal setting with an additional set of measurements18,20,21.
When accounting for the noise, the proposed technique thus requires only 7 measurements instead of the conventional 16: 3 measurements in the lattice space, 3 in the reciprocal space, and a last one, still in the reciprocal space, to fix normalization and remove all the ambiguities on the parameters of the unitary.
Experimental results
In photonic setups, a qubit can be encoded into photon polarization, which is typically manipulated via optical waveplates. In the circular polarization basis, where \(\left\vert L\right\rangle ={(1,0)}^{T}\) and \(\left\vert R\right\rangle ={(0,1)}^{T}\) are left and right circular polarization states, respectively, a waveplate Lδ,θ having the birefringence δ and the optic axis oriented at θ with respect to the horizontal direction can be expressed in the matrix form:
A single waveplate thus implements a rotation of an angle −δ/2 around the equatorial axis \({{{\bf{n}}}}=(\cos 2\theta ,\sin 2\theta ,0)\). Nevertheless, one can cascade multiple waveplates to implement more general operations35,36.
We apply FQPT to periodic polarization transformations induced by complex LCMSs22. These can be modeled as optical waveplates having patterned optic-axis modulation θ = θ(x, y) and fixed, but tunable, birefringence37. In particular, we test our method with LCMSs featuring high spatial-frequency modulations along the x and y directions. This scenario is experimentally more challenging than the one addressed in ref. 18, where simple combinations of polarization gratings were considered. We benchmark our technique against the standard ML approach processing a whole set of 16 polarimetric measurements (all taken in the near field), taking into account both the timing and the accuracy of the final reconstruction. For the minimization, we employed the NMinimize routine from Wolfram Mathematica38.
The experiments are realized with the setup sketched in Fig. 1a. A Ti:Sa laser (wavelength λ = 810 nm) is coupled to a single-mode fiber. The output Gaussian mode is magnified with a telescope lens system, f1 = 125 mm and f2 = 200 mm (not shown in the figure). The beam waist is measured to be 2.6 ± 0.1 mm. In this way, the overall beam size is larger than the largest periodicity on the plates, that is Λ = 2.5 mm. A combination of a linear polarizer (P1), a half-wave plate (HWP1) and a quarter-wave plate (QWP1) is needed to prepare any input polarization state. The beam then propagates through one or multiple LCMSs, engineering a space-dependent SU(2) optical operator. Another set QWP2-HWP2-P2 is adjusted to project onto any state. The last element (P2) is removed when performing the measurement of Eq. (7). Each polarimetric measurement is collected on a CCD camera, placed either after a 4f system (f = 150 mm) or in the focal plane of a lens (\({f}^{{\prime} }=250\,{{\mbox{mm}}}\,\)), depending on if the measurement is realized in the near field or in the far field, respectively. Recall that the far-field light distribution is proportional to the transverse momentum distribution, i.e., to the Fourier transform of the input field.
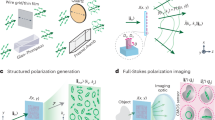
a A space-dependent polarization transformation U(x, y) is implemented via LCMSs. The process tomography is performed by preparing and projecting onto MUB states. The resulting intensity distributions are measured in the far field, \({\tilde{I}}_{aa}({k}_{x},{k}_{y})\), and the image plane, Iaa(x, y), of the optical operator. b Plots of the optic-axis pattern of two plates used to test the technique. These are patterned along orthogonal directions to create a complex 2D modulation. c Reconstruction of the process U(x, y) = Tx(x)Ty(y) using FQPT and the traditional ML technique. The arrows represent the local eigenvectors n(x, y) and their color is associated with the local rotation angle E(x, y) (see also Fig. 3d for details).
The first experiment is realized with a single LCMS displaying a complex periodic modulation along the x axis (see Fig. 1b). The optical retardation is set at δ = π. The periodicity of the process simplifies the analysis, as only a discrete spectrum of Fourier components is expected to appear in the far field for all the measurements. Furthermore, in this one-dimensional (1D) realization, the intensity modulations can also be integrated along the y direction to mitigate experimental imperfections.
Figure 2a shows the far-field intensity distributions recorded for the 〈H∣U∣H〉 configuration, with \(\left\vert H\right\rangle =(\left\vert L\right\rangle +\left\vert R\right\rangle )/\sqrt{2}\). As discussed above, the far-field distribution can be discretized and a normalized power spectrum P(m) is extracted. Figure 2b, c illustrates the comparison between the experimentally measured total far-field distribution for a \(\left\vert L\right\rangle\) input state (see Eq. (7)) and the reconstruction performed via FQPT and ML, respectively. The agreement with the experimental observation is quantified in terms of the similarity estimator \(s={({\sum }_{m}\sqrt{{P}_{\exp }(m){P}_{{{{\rm{rec}}}}}(m)})}^{2}\), where \({P}_{\exp }(m)\) and Prec(m) are the (normalized) experimental and reconstructed far-field distributions. We obtain sFQPT = 97.2% and sML = 97.0%. Another metric that can be considered is the absolute distance between the two distributions, computed as \({{\Delta }}={({\sum }_{m}| {P}_{\exp }(m)-{P}_{{{{\rm{rec}}}}}(m)| )}^{2}\). We report ΔFQPT = 0.088 and ΔML = 0.083. In both figures, the insets show the same comparison for the 1D near-field amplitude \(\sqrt{{I}_{HH}(x)}\). Reconstructions of individual parameters are plotted in Fig. 2d. We note that the reconstruction of E suffers from higher deviations from the ML prediction, while this does not occur for the vector n. This is ascribed to the role of the unit-norm constraint, which further restricts the optimization domain for the vector n. The agreement between the predictions of the two methods is quantified in terms of the fidelity \(F=| {{{\rm{Tr}}}}({U}_{{{{\rm{ML}}}}}^{{\dagger} }{U}_{{{{\rm{FQPT}}}}})| /n\), where n = 2 is the dimension of the internal degree of freedom39. An excellent average fidelity is obtained, \(\bar{F}=95.7 \%\), where \(\bar{F}\) denotes the average fidelity computed over all the pixels. These results prove that both methods provide reliable reconstructions. It must be noted that FQPT achieves satisfactory reconstructions by only processing a near-optimal set of measurements. Moreover, a brute-force minimization approach tends to jump between the parameters associated with processes U and eiπU = −U, as these both generate the same experimental outcomes18,40,41,42. For this reason, a continuity constraint must be enforced between consecutive pixels. Conversely, our method only relies on the block-diagonal decomposition of the complex unitary operator. The technique is also extremely efficient on the computational level. The total times required for a complete reconstruction are \({t}_{{{{\rm{FQPT}}}}}^{1{{{\rm{D}}}}}\,\approx\, 1\,{{\mbox{min}}}\,\) and \({t}_{{{{\rm{ML}}}}}^{{{{\rm{1D}}}}}\approx 30\,{{\mbox{min}}}\,\).
a Far-field intensity distribution \({\tilde{I}}_{HH}({k}_{x})\) for a 1D periodic SU(2) transformation. A power spectrum P(m) is extracted after discretizing the reciprocal space. Comparison between the experimental total far-field distribution for a \(\left\vert L\right\rangle\) input state and the reconstruction obtained from FQPT (b) and ML (c). The insets show the reconstructed near-field amplitude \(\sqrt{{I}_{HH}(x)}\), compared with the experimental measurement. d Reconstructions of the process parameters across one period performed by FQPT (red curves) and ML (blue curves). The expected periodicity is captured by both approaches.
Recall that the GS algorithm is executed to retrieve the unknown phases. This algorithm is based on an iterative strategy that presents intrinsic limitations43. The convergence speed is sensitive to the initial guess of the phase, and the convergence to a global minimum is not guaranteed. Moreover, the presence of noise in the input data can severely affect the accuracy of phase retrieval. To overcome these limitations, for each set of polarimetric measurements, the algorithm is run \({N}_{T}^{{{{\rm{1D}}}}}=100\) times for \({N}_{I}^{{{{\rm{1D}}}}}=1000\) iterations, randomly initializing the phase guess at each trial. In doing so, the best phase reconstruction can be selected (up to global shifts) as the one minimizing the total distance between the reconstructed and measured near-field amplitudes. The number of repetitions is chosen to ensure the stability of the final reconstruction. Alternatively, the routine can be stopped when the algorithm has converged below a tolerance threshold.
The second experiment is realized by cascading the previous LCMS with a second one, patterned along the y direction (see Fig. 1b). The sequence thus implements a two-dimensional (2D) periodic SU(2) transformation. The birefringence setting is δ1 = π/2 and δ2 = π. Figure 3a shows the experimental far-field distribution \({\tilde{I}}_{HH}({k}_{x},{k}_{y})\), from which a 2D power spectrum P(mx, my) is extracted. The total far-field reconstructions for a \(\left\vert L\right\rangle\) input state are plotted in Fig. 3c, where the comparison with the experimental result is also provided. We obtain sFQPT = 88.5% and sML = 96.7%, with a total error of ΔFQPT = 0.080 and ΔML = 0.013. The slight deterioration in the final prediction can be ascribed to the reduced performance of the GS algorithm in two spatial dimensions44. Figure 3b shows the near-field amplitude \(\sqrt{{I}_{HH}(x,y)}\), as reconstructed from FQPT and ML, compared with the experimental measurement. In this case, the GS algorithm runs \({N}_{T}^{{{{\rm{2D}}}}}=50\) times for \({N}_{I}^{{{{\rm{2D}}}}}=500\) iterations. In this realization, we compress the experimental images by integrating light intensity over 11 pixel × 11 pixel regions equally distributed on the camera. This allows for both minimizing the errors due to local intensity fluctuations in the image area and keeping the computation time within the same range as the 1D experiment. The reconstructions of individual parameters are shown in Fig. 3d. An alternative visualization of the reconstructed process in terms of the local eigenvector and rotation angle is provided in Fig. 1c. A good agreement is observed between the two predictions, with average fidelity \(\bar{F}=91.4 \%\). The computation times are \({t}_{{{{\rm{FQPT}}}}}^{{{{\rm{2D}}}}}\,\approx\, 5\,{{\mbox{min}}}\,\) and \({t}_{{{{\rm{ML}}}}}^{{{{\rm{2D}}}}}\,\approx\, 60\,{{\mbox{min}}}\,\).
a Far-field intensity distribution \({\tilde{I}}_{HH}({k}_{x},{k}_{y})\) for a 2D periodic SU(2) transformation. A power spectrum P(mx, my) is extracted. b Reconstructed near-field amplitude \(\sqrt{{I}_{HH}(x,y)}\), compared with the experimental measurement. c Comparison between the total far-field distribution for a \(\left\vert L\right\rangle\) input state and the reconstruction obtained from FQPT and ML. d Reconstructions of the process parameters across one period performed by FQPT and ML. The expected periodicity is captured by both approaches.
Discussion
In this work, a technique for fast and accurate Quantum Process Tomography is demonstrated. This is accomplished via a non-interferometric scheme requiring no a-priori information on the unknown operator. In the case of complex polarization transformations, our method achieves performances very close to the standard tomography based on an overcomplete set of measurements. It offers experimental advantage, only requiring a near-minimal set of measurements, and computational speed-up, outperforming the standard approach by at least one order of magnitude. The proposed scheme relies on a standard phase retrieval algorithm and does not require a careful fine-tuning of hyperparameter configurations, which is instead crucial in typical optimization routines18.
FQPT appears naturally suitable for all experimental setups that allow for easy access to conjugate domains. The implementation of the QFT algorithm in non-optical setups is still challenging, however more efficient protocols based on digital-analog computing45, cold atoms in reprogrammable lattices46, and dynamic circuits47 have recently been proposed. For this reason, this method could also be soon implemented on other physical platforms, such as quantum circuits for atoms48,49 and electron beams50,51.
Nevertheless, we believe that the performance of the method can be further improved by adopting optimized strategies for phase retrieval. For instance, convolutional neural networks represent a promising solution52,53,54. We also expect that FQPT can detect non-unitary evolutions55 if equipped with some minor modifications, such as including multiple intermediate planes in the final analysis. At the same time, it would be interesting to adapt the present method to retrieve multi-photon gates and complex operations in high-dimensional Hilbert spaces.
In principle, this procedure can also be applied to processes acting on a m × d dimensional space, having the irreducible form \({\bigoplus }_{i = 1}^{d}{{{{\mathcal{U}}}}}^{(i)}\), with \({{{{\mathcal{U}}}}}^{(i)}\in \,{{\mbox{SU}}}\,(m)\). In this case, one must consider the decomposition of \({{{{\mathcal{U}}}}}^{(i)}\) in the generators of SU(m), the generalized Gell-Mann matrices. Although the analytical relations between the process parameters and the measurement outcomes become significantly more complicated, the number of measurements required by FQPT will still be optimal. This will be investigated in successive works.
Data availability
The data supporting the findings of this study are available in ref. 56.
Code availability
The code for data processing is available in ref. 56.
References
Chuang, I. L. & Nielsen, M. A. Prescription for experimental determination of the dynamics of a quantum black box. J. Mod. Opt. 44, 2455 (1997).
Childs, A. M., Chuang, I. L. & Leung, D. W. Realization of quantum process tomography in NMR. Phys. Rev. A 64, 012314 (2001).
Myrskog, S. H., Fox, J. K., Mitchell, M. W. & Steinberg, A. M. Quantum process tomography on vibrational states of atoms in an optical lattice. Phys. Rev. A 72, 013615 (2005).
Roos, C. F. et al. Bell states of atoms with ultralong lifetimes and their tomographic state analysis. Phys. Rev. Lett. 92, 220402 (2004).
Riebe, M. et al. Process tomography of ion trap quantum gates. Phys. Rev. Lett. 97, 220407 (2006).
Yamamoto, T. et al. Quantum process tomography of two-qubit controlled-Z and controlled-NOT gates using superconducting phase qubits. Phys. Rev. B 82, 184515 (2010).
Bialczak, R. C. et al. Quantum process tomography of a universal entangling gate implemented with Josephson phase qubits. Nat. Phys. 6, 409 (2010).
Mitchell, M. W., Ellenor, C. W., Schneider, S. & Steinberg, A. M. Diagnosis, prescription, and prognosis of a Bell-state filter by quantum process tomography. Phys. Rev. Lett. 91, 120402 (2003).
Altepeter, J. B. et al. Ancilla-assisted quantum process tomography. Phys. Rev. Lett. 90, 193601 (2003).
O’Brien, J. L. et al. Quantum process tomography of a controlled-NOT gate. Phys. Rev. Lett. 93, 080502 (2004).
Lobino, M. et al. Complete characterization of quantum-optical processes. Science 322, 563 (2008).
Bongioanni, I., Sansoni, L., Sciarrino, F., Vallone, G. & Mataloni, P. Experimental quantum process tomography of non-trace-preserving maps. Phys. Rev. A 82, 042307 (2010).
Rahimi-Keshari, S. et al. Direct characterization of linear-optical networks. Opt. Express 21, 13450 (2013).
Ndagano, B. et al. Characterizing quantum channels with non-separable states of classical light. Nat. Phys. 13, 397 (2017).
Antón, C. et al. Tomography of the optical polarization rotation induced by a single quantum dot in a cavity. Optica 4, 1326 (2017).
Jacob, K. V., Mirasola, A. E., Adhikari, S. & Dowling, J. P. Direct characterization of linear and quadratically nonlinear optical systems. Phys. Rev. A 98, 052327 (2018).
Bouchard, F. et al. Quantum process tomography of a high-dimensional quantum communication channel. Quantum 3, 138 (2019).
Di Colandrea, F., Amato, L., Schiattarella, R., Dauphin, A. & Cardano, F. Retrieving space-dependent polarization transformations via near-optimal quantum process tomography. Opt. Express 31, 31698 (2023).
Le Roy-Brehonnet, F. & Le Jeune, B. Utilization of Mueller matrix formalism to obtain optical targets depolarization and polarization properties. Prog. Quantum Electron. 21, 109 (1997).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Aiello, A., Puentes, G., Voigt, D. & Woerdman, J. P. Maximum-likelihood estimation of Mueller matrices. Opt. Lett. 31, 817 (2006).
Di Colandrea, F. et al. Ultra-long quantum walks via spin-orbit photonics. Optica 10, 324 (2023).
Goodman, J. W. Introduction to Fourier Optics (Roberts and Company Publishers, 2005).
Wang, J., Sciarrino, F., Laing, A. & Thompson, M. G. Integrated photonic quantum technologies. Nat. Photonics 14, 273 (2020).
Politi, A., Matthews, J. C. & O’Brien, J. L. Shor’s quantum factoring algorithm on a photonic chip. Science 325, 1221 (2009).
Crespi, A. et al. Suppression law of quantum states in a 3D photonic fast Fourier transform chip. Nat. Commun. 7, 10469 (2016).
Flamini, F. et al. Observation of photonic states dynamics in 3-D integrated Fourier circuits. J. Opt. 20, 074001 (2018).
Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).
Heilmann, R., Gräfe, M., Nolte, S. & Szameit, A. Arbitrary photonic wave plate operations on chip: realizing Hadamard, Pauli-X and rotation gates for polarisation qubits. Sci. Rep. 4, 4118 (2014).
Pitsios, I., Samara, F., Corrielli, G., Crespi, A. & Osellame, R. Geometrically-controlled polarisation processing in femtosecond-laser-written photonic circuits. Sci. Rep. 7, 11342 (2017).
Weinstein, Y. S., Pravia, M., Fortunato, E., Lloyd, S. & Cory, D. G. Implementation of the quantum Fourier transform. Phys. Rev. Lett. 86, 1889 (2001).
Fowler, A. G., Devitt, S. J. & Hollenberg, L. C. Implementation of Shor’s algorithm on a linear nearest neighbour qubit array. Quantum Info. Comput. 4, 237–251 (2004).
Mariantoni, M. et al. Implementing the quantum von Neumann architecture with superconducting circuits. Science 334, 61 (2011).
Gerhberg, R. & Saxton, W. A practical algorithm for the determination of phase from image and diffraction plane picture. Optik 35, 237 (1972).
Simon, R. & Mukunda, N. Minimal three-component SU(2) gadget for polarization optics. Phys. Lett. A 143, 165 (1990).
Sit, A., Giner, L., Karimi, E. & Lundeen, J. S. General lossless spatial polarization transformations. J. Opt. 19, 094003 (2017).
Rubano, A., Cardano, F., Piccirillo, B. & Marrucci, L. Q-plate technology: a progress review [Invited]. J. Opt. Soc. Am. B 36, D70 (2019).
Wolfram Research. Numerical Nonlinear Global Optimization (2021).
Wang, X., Sun, Z. & Wang, Z. D. Operator fidelity susceptibility: an indicator of quantum criticality. Phys. Rev. A 79, 012105 (2009).
Fläschner, N. et al. Experimental reconstruction of the Berry curvature in a Floquet Bloch band. Science 352, 1091 (2016).
Tarnowski, M. et al. Measuring topology from dynamics by obtaining the Chern number from a linking number. Nat. Commun. 10, 1728 (2019).
Yi, C.-R. et al. Extracting the quantum geometric tensor of an optical Raman lattice by Bloch-state tomography. Phys. Rev. Res. 5, L032016 (2023).
Fienup, J. R. Phase retrieval algorithms: a comparison. Appl. Opt. 21, 2758 (1982).
Zhao, T. & Chi, Y. Modified Gerchberg-Saxton (G-S) algorithm and its application. Entropy 22, 1354 (2020).
Martin, A., Lamata, L., Solano, E. & Sanz, M. Digital-analog quantum algorithm for the quantum Fourier transform. Phys. Rev. Res. 2, 013012 (2020).
Wang, P., Huang, Z., Qiu, X. & Li, X. Programmable Hamiltonian engineering with quadratic quantum Fourier transform. Phys. Rev. B 106, 134313 (2022).
Bäumer, E., Tripathi, V., Seif, A., Lidar, D. & Wang, D. S. Quantum Fourier transform using dynamic circuits. Preprint at http://arxiv.org/abs/2403.09514 (2024).
Guidoni, L. & Verkerk, P. Optical lattices: cold atoms ordered by light. J. Opt. B Quantum Semiclass. Opt. 1, R23 (1999).
Gross, C. & Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 357, 995 (2017).
Harris, J. et al. Structured quantum waves. Nat. Phys. 11, 629 (2015).
Grillo, V. et al. Holographic generation of highly twisted electron beams. Phys. Rev. Lett. 114, 034801 (2015).
White, J., Wang, S., Eschen, W. & Rothhardt, J. Real-time phase-retrieval and wavefront sensing enabled by an artificial neural network. Opt. Express 29, 9283 (2021).
Li, B. et al. Phase retrieval based on difference map and deep neural networks. J. Mod. Opt. 68, 1108 (2021).
Ding, G. et al. Spatial phase retrieval of vortex beam using convolutional neural network. J. Opt. 24, 025701 (2022).
Wang, C. et al. Non-Hermitian optics and photonics: from classical to quantum. Adv. Opt. Photon. 15, 442 (2023).
Di Colandrea, F., Dehghan, N., D’Errico, A. & Karimi, E. https://github.com/FraDiColandrea/Fourier_Quantum_Process_Tomography.
Acknowledgements
This work was supported by the Canada Research Chair (CRC) Program, NRC-uOttawa Joint Centre for Extreme Quantum Photonics (JCEP) via the Quantum Sensors Challenge Program at the National Research Council of Canada, and Quantum Enhanced Sensing and Imaging (QuEnSI) Alliance Consortia Quantum grant.
Author information
Authors and Affiliations
Contributions
F.D.C. conceived the idea, developed the theory, and performed numerical simulations. F.D.C., N.D. and A.D.E. fabricated the plates and performed the experiment. F.D.C. and N.D. analyzed the data. A.D.E. and E.K. supervised the project. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Colandrea, F., Dehghan, N., D’Errico, A. et al. Fourier Quantum Process Tomography. npj Quantum Inf 10, 49 (2024). https://doi.org/10.1038/s41534-024-00844-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-024-00844-7